紙からつくる

京都伏見アトリエ遊では、多面体をつくっています。
一度つくってみませんか？
簡単にできます。
ユニットで繰り返せば、工作は５歳から。コンパスや定規を使えばますます勉強にもなるしね。

http://ja.wikipedia.org/wiki/%E6%AD%A3%E5%A4%9A%E9%9D%A2%E4%BD%93
多面体の説明です
……………………………………………………………….
正多面体の表面積、体積は一辺を a とすれば、概略下記となる。

名前と図	構成面	辺	頂点	シュレーフリ記号	表面積とその概数	体積とその概数
正四面体	正三角形	6	4	{3,3}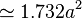
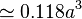正六面体	正方形	12	8	{4,3}
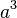正八面体	正三角形	12	6	{3,4}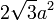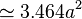
正十二面体	正五角形	30	20	{5,3}
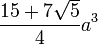正二十面体	正三角形	30	12	{3,5}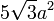

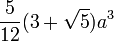双対[編集]

正多面体は、適切に頂点を選ぶことで別の正多面体を作ることができる。 代表的なものは各面の中心を結ぶという操作で、

• 正二十面体 ↔ 正十二面体
• 正六面体 ↔ 正八面体
• 正四面体 ↔ 正四面体

の様に作ることが出来る。これらの関係を双対という。このうち正四面体は正四面体自身になる（自己双対）。
ほかには、

• 正六面体の1つおきの頂点 → 正四面体
• 正十二面体の適当な頂点 → 正四面体、正六面体
• 正四面体の各辺の中点 → 正八面体
• 正八面体の各辺を黄金分割して結ぶ → 正二十面体

などがある。

星型正多面体というものもある。
…………………………………………………………………..

 

これは、サッカーボールで多面体ではないですが、
コンパスをうまく使えば簡単にできます。

まだまだ、アトリエには色々な方法で立体基礎を学びます。